Problem C1.5. Radial Expansion Wave (2D or 3D)
ATTENTION!
It has been brought to our attention that the flow described below in 2D on fine grids develops a kink before t=3, so that it ceases to be a suitable test problem for evaluating the high order of accuracy of a method. It is recommended to do the error analysis at t=2 instead.
In the 3D case, moving the analysis to the earlier time helps somewhat to limit the loss of accuracy, but is not a full remedy. At present it is not quite clear what causes the breakdown of accuracy in 3D; it is being investigated further. Possibly, nonradial instabilities are involved.
One suggestion is to run codes at gamma = 3. This nonphysical specific-heat ratio tends to decouple the acoustic modes and may postpone nonlinear complications.
Overview
This time-dependent radial flow is entirely determined by its initial values. These show a cylindrical (2D) or spherical (3D) expansion wave ready to move toward the origin and interact with itself. There are no walls and there is no influence of the domain boundary, owing to supersonic outflow everywhere.
Governing Equations
The governing equation is the 2D or 3D Euler equations with a constant ratio of specific heats of g = g = 1.4.
Flow Conditions
The initial condition is defined everywhere. The flow is cylindrically (2D) or spherically (3D) symmetric but computed on a Cartesian grid. The flow field is purely radial. The initial distribution of the radial velocity q is infinitely differentiable:
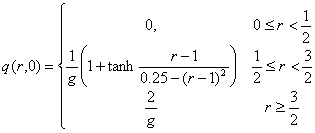
The Cartesian velocity components are related to q at any time and place by
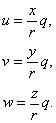
The initial distribution of the speed of sound a derives from q(r, 0):
![]()
here the ratio of specific heats may be chosen by the user from the interval 1 < g < 3, e. g. = 7/5 (aero), = 5/3 (astro), = 2 (civil, atmospheric). For this workshop, g = 7/5. The density initially equals g in the origin and further follows from assuming uniform entropy:
![]()
The initial values of any other flow quantity derive from the above equations and the perfect-gas law, e. g., pressure:
![]() .
.
Because the flow is entirely determined by the initial values, these should be carefully discretized. For instance, if the numerical method is a finite-volume scheme that uupdates the cell-averages of the conserved flow quantities, these must be computed from the analytical initial values by a sufficiently accurate Gaussian quadrature. The same holds for the integrals needed to compute the weights of the basis functions in a Discontinuous Galerkin discretization. If superconvergence is anticipated, the order of accuracy of the Gaussian quadrature must be taken high enough so as not to obscure the truncation error of the scheme with an initialization error.
At outflow the Mach number is 2, which means supersonic outflow normal to all domain boundaries, in both 2D and 3D.
Geometry
The computational domain is a square (cube) [−4, 4] í┴[−4, 4] (í┴[−4, 4]), uniformly divided into cells with Dx = Dy (=Dz) = h, where h takes the values 1/8 (grid 1), 1/16 (grid 2), 1/32 (grid 3), etc. The simulations should be run from t=0 to t=3. The largest wave speed appearing in the problem is 3/g, which may be helpful in setting the time step. However, tests should be performed to ensure that the time step is small enough (or the order of time integration is high enough) that temporal resolution has minimal effect on the results.
Boundary Conditions
Supersonic outflow everywhere.
Requirements
1. At the initial time (t=0) and at the final time (t=3), compute the L2-norm of the error in the cell-average of the entropy. Compute the local entropy error as
![]()
In
each cell, compute the average ![]() of this error by Gaussian quadrature of
its subcell distribution. Note that for a
finite-volume method you must first perform the methodí»s standard subcell interpolation, as if starting a new time-step. The error
norm is defined as usual:
of this error by Gaussian quadrature of
its subcell distribution. Note that for a
finite-volume method you must first perform the methodí»s standard subcell interpolation, as if starting a new time-step. The error
norm is defined as usual:

where the sum is taken over all (N) cells.
2. Study
the numerical order of accuracy according to ![]() vs.
vs. ![]()
3. Submit the following data to the workshop for this case
a. ![]() error vs. work units for different h and p at t=0 and t=3
error vs. work units for different h and p at t=0 and t=3
b. ![]() error vs
error vs ![]() for different h and p at t=0 and t=3
for different h and p at t=0 and t=3
c. A time history figure showing ![]() (log scale) versus time for
different h and p.
(log scale) versus time for
different h and p.
Further Error Analysis
Because the solution is infinitely smooth and the grid is Cartesian, the numerical solution to this problem lends itself especially well to Richardson extrapolation. That is, solutions obtained on a sequence of grids may serve, after prolongation of the finer-grid solutions to the coarsest grid, to find an expansion of the local truncation on the coarsest grid in powers of the mesh width. A good choice of flow quantity for this process is the density, since all FV and FE codes update directly the cell-averaged density; no Gaussian quadrature is needed. This type of error analysis is elective.